
Recently, I came up with an idea for a new Optimizer (an algorithm for training neural network). In theory, it looked great but when I implemented it and tested it, it didn’t turn out to be good.
Some of my learning are:
- Neural Networks are hard to predict.
- Figuring out how to customize TensorFlow is hard because the main documentation is messy.
- Theory and Practical are two different things. The more hands-on you are, the higher are your chances of trying out an idea and thus iterating faster.
I am sharing my algorithm here. Even though this algorithm may not be of much use to you but it would give you ideas on how to implement your own optimizer using Tensorflow Keras.
A neural network is basically a set of neurons connected to input and output. We need to adjust the connection strengths such that it gives the least error for a given set of input. To adjust the weight we use the algorithms. One brute force algorithm could be to try all possible combinations of weights (connections strength) but that will be too time-consuming. So, we usually use the greedy algorithm most of these are variants of Gradient Descent. In this article, we will write our custom algorithm to train a neural network. In other words, we will learn how to write our own custom optimizer using TensorFlow Keras.
Gradient descent is simply this:
New_weight = weight - eta * rate of change of error wrt weight
w -= η*∂E/∂wHere eta (learning rate) is basically some constant. We will need to figure out. Usually, we keep eta as 0.001.
Here is an easy way to visualize it. If there is only one weight, we can visualize it like this:
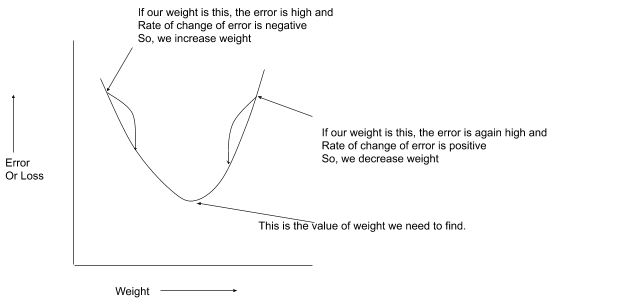
In this blog, we will learn how to create your own algorithm. Though it is extremely rare to need to customize the optimizer there are around 5-6 variants of Gradient descent algorithm but again if you get an idea of a new clever optimizer it could be a breakthrough.
In Gradient Descent, if the eta or learning rate is too high the error might increase instead of decreasing because the next value of weight could go to the other side of minima.
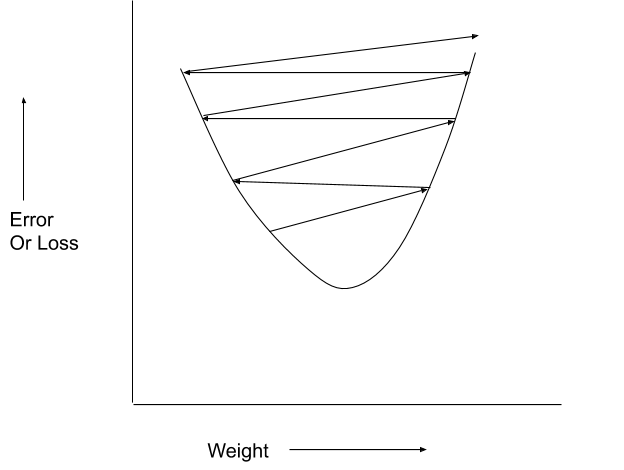
In my optimizer, I thought that the moment the slope changes sign, we will average the weight.
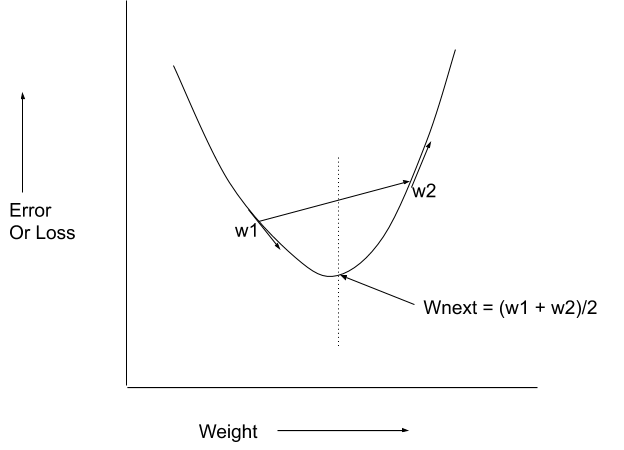
If the slope hasn’t changed the sign, the usual gradient descent will apply.
Now, let us get to the coding.
First import the libraries that we will be using.
import tensorflow as tf
from tensorflow import keras
# Common imports
import numpy as np
import os
We are going to test our optimizer on California housing data. Now, let us load the data and create test and training data sets.
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(
housing.data, housing.target.reshape(-1, 1), random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(
X_train_full, y_train_full, random_state=42)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_valid_scaled = scaler.transform(X_valid)
X_test_scaled = scaler.transform(X_test)
In order to create a custom optimizer we will have to extend from base Optimizer Class which is in keras.optimizers class.
class SGOptimizer(keras.optimizers.Optimizer):
…
<< this is where our implementation would be >>>
…
We will be overriding or implementing these methods:
- __init__ – Constructor
- _create_slots
- _resource_apply_dense
- _resource_apply_sparse (just marking it not-implemented)
- get_config
Constructor – __init__ method
Whenever we define a class in Python, we define a constructor with a name __init__ (starts and ends with double dashes). This method should have the first argument as ‘self’ which basically will point to the object. The remaining arguments are your own choice. You can supply these arguments at the time of creating the object of this. Here we usually define the hyperparameters. In our cases, we don’t have any other hyperparameters than the learning_rate. The default value of the learning rate we are setting as 0.01. In case, we don’t supply the learning_rate argument it would assume it to be 0.01. The name argument is something used by the system for displaying progress etc. The remaining arguments are absorbed by kwargs and passed to the parent as is.
Here, we are delegating work to the parent class that is Optimizer by the way of calling super(). First we are creating the base class by calling __init__() method on super(). Notice that we are sending “name” and “kwargs” to the parent.
Afterwards, we are setting the hyperparameter learning rate by calling _set_hyper. Notice that if someone provides ‘lr’ also in arguments, that would take preference over learning_rate.
Also, notice that we are setting _is_first to be true. We don’t want to use our algorithm for the first time because we need to compare the current gradient with previous if there signs are different.
def __init__(self, learning_rate=0.01, name="SGOptimizer", **kwargs):
"""Call super().__init__() and use _set_hyper() to store hyperparameters"""
super().__init__(name, **kwargs)
self._set_hyper("learning_rate", kwargs.get("lr", learning_rate)) # handle lr=learning_rate
self._is_first = True
The next important method to implement is _create_slots. A slot is basically a placeholder where we will keep extra value. A slot is per variable where a variable could be weight or bais. We would need two slots extra – one for keeping track of the previous gradient so that we can compare if the previous gradient sign was different from current. We need another slot for keeping previous weight (or variable value) so that we can compute the average of current weight and previous if the signs of gradient are different. Every slot has a name. The names of our slot are “pv” and “pg”.
def _create_slots(self, var_list):
"""For each model variable, create the optimizer variable associated with it.
TensorFlow calls these optimizer variables "slots".
For momentum optimization, we need one momentum slot per model variable.
"""
for var in var_list:
self.add_slot(var, "pv") #previous variable i.e. weight or bias
for var in var_list:
self.add_slot(var, "pg") #previous gradient
Now, let us implement the main algorithm by the way of _resource_apply_dense. This method is called on every step. It provides your two variables grad and var. Both grad and var are basically tensors (or vectors) and contain the value of gradients (rate of change of loss wrt variable) and the variables. This method is called per layer but you don’t have to worry about that part since you are dealing with tensors.
Remaining implementation is straight forward. Not @tf.function at the top, it is a signal to tensorflow to convert the function to tensorflow graph.
@tf.function
def _resource_apply_dense(self, grad, var):
"""Update the slots and perform one optimization step for one model variable
"""
var_dtype = var.dtype.base_dtype
lr_t = self._decayed_lr(var_dtype) # handle learning rate decay
# Compute the new weight using the traditional gradient descent method
new_var_m = var - grad * lr_t
# Extract the previous values of Variables and Gradients
pv_var = self.get_slot(var, "pv")
pg_var = self.get_slot(var, "pg")
# If it first time, use just the traditional method
if self._is_first:
self._is_first = False
new_var = new_var_m
else:
# create a boolean tensor contain true and false
# True will be where the gradient haven't changed the sign and False will be the case where the gradients have changed sign
cond = grad*pg_var >= 0
# Compute the average of previous weight and current. Though we will be using only few of these.
#Of course, it is prone to overflow. We can also compute the avg using a + (b -a)/2.0
avg_weights = (pv_var + var)/2.0
# tf.where picks the value from new_var_m where the cond is True otherwise it takes from avg_weights
# We must avoid the for loops
new_var = tf.where(cond, new_var_m, avg_weights)
# Finally we are saving current values in the slots.
pv_var.assign(var)
pg_var.assign(grad)
# We are updating weight here. We don't need to return anything
var.assign(new_var)
The complete class would look like this:
class SGOptimizer(keras.optimizers.Optimizer):
def __init__(self, learning_rate=0.01, name="SGOptimizer", **kwargs):
"""Call super().__init__() and use _set_hyper() to store hyperparameters"""
super().__init__(name, **kwargs)
self._set_hyper("learning_rate", kwargs.get("lr", learning_rate)) # handle lr=learning_rate
self._is_first = True
def _create_slots(self, var_list):
"""For each model variable, create the optimizer variable associated with it.
TensorFlow calls these optimizer variables "slots".
For momentum optimization, we need one momentum slot per model variable.
"""
for var in var_list:
self.add_slot(var, "pv") #previous variable i.e. weight or bias
for var in var_list:
self.add_slot(var, "pg") #previous gradient
@tf.function
def _resource_apply_dense(self, grad, var):
"""Update the slots and perform one optimization step for one model variable
"""
var_dtype = var.dtype.base_dtype
lr_t = self._decayed_lr(var_dtype) # handle learning rate decay
new_var_m = var - grad * lr_t
pv_var = self.get_slot(var, "pv")
pg_var = self.get_slot(var, "pg")
if self._is_first:
self._is_first = False
new_var = new_var_m
else:
cond = grad*pg_var >= 0
print(cond)
avg_weights = (pv_var + var)/2.0
new_var = tf.where(cond, new_var_m, avg_weights)
pv_var.assign(var)
pg_var.assign(grad)
var.assign(new_var)
def _resource_apply_sparse(self, grad, var):
raise NotImplementedError
def get_config(self):
base_config = super().get_config()
return {
**base_config,
"learning_rate": self._serialize_hyperparameter("learning_rate"),
}
def _resource_apply_sparse(self, grad, var):
raise NotImplementedError
def get_config(self):
base_config = super().get_config()
return {
**base_config,
"learning_rate": self._serialize_hyperparameter("learning_rate"),
"decay": self._serialize_hyperparameter("decay"),
"momentum": self._serialize_hyperparameter("momentum"),
}
Now, let us test it. Let us first clear the tensorflow session and reset the the random seed:
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)Let us fire up the training now. First we create a simple neural network with one layer and call compile by setting the loss and optimizer. Notice that we are passing the object of our optimizer. Finally call, model.fit.
model = keras.models.Sequential([keras.layers.Dense(1, input_shape=[8])])
model.compile(loss="mse", optimizer=SGOptimizer(learning_rate=0.001))
model.fit(X_train_scaled, y_train, epochs=50)This is the output:
Train on 11610 samples
Epoch 1/50
Tensor("GreaterEqual:0", shape=(1,), dtype=bool)
11610/11610 [==============================] - 1s 95us/sample - loss: 3.7333
Epoch 2/50
11610/11610 [==============================] - 1s 47us/sample - loss: 1.4848
Epoch 3/50
11610/11610 [==============================] - 1s 48us/sample - loss: 0.9218
…
…
Epoch 47/50
11610/11610 [==============================] - 1s 45us/sample - loss: 0.5306
Epoch 48/50
11610/11610 [==============================] - 1s 45us/sample - loss: 0.5317
Epoch 49/50
11610/11610 [==============================] - 1s 47us/sample - loss: 0.5311
Epoch 50/50
11610/11610 [==============================] - 1s 46us/sample - loss: 0.5312
If you compare this trend of loss against the usual gradient descent or any of the variants of it, you will realize that it is not an improvement.
The complete code is available in this repository: https://github.com/cloudxlab/ml/blob/master/exp/Optimizer_2.ipynb
To learning more, visit CloudxLab.com.